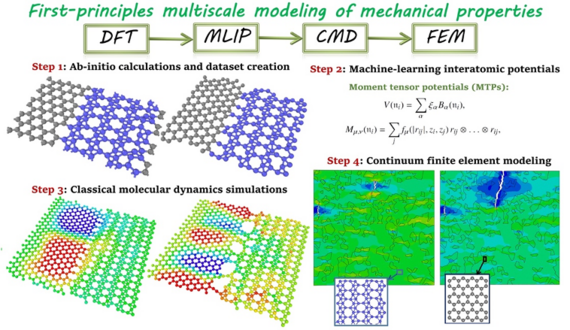
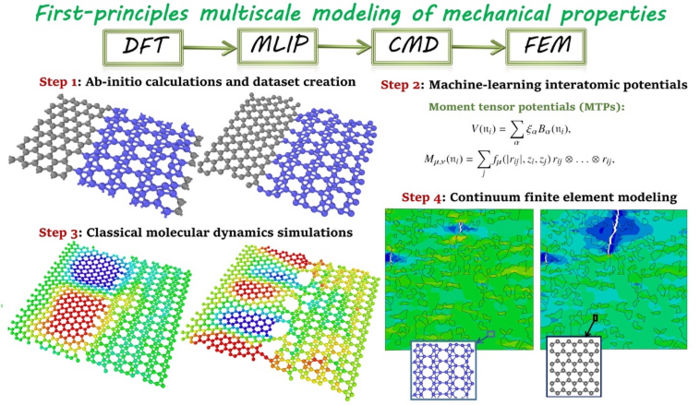
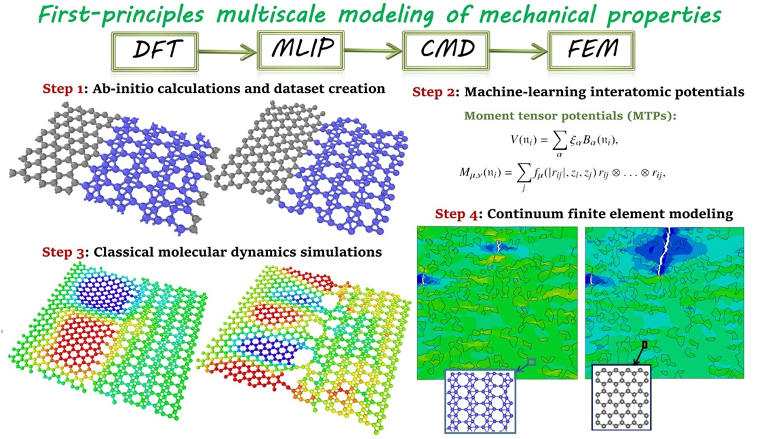
A key task for materials design is to search and characterize candidate materials that can fulfill specific requirement of performance. In this direction, the multiscale modelling and machine learning approach for finding, characterizing and designing new materials is explored. High computational cost is always an issue in multiscale modelling, especially high computational cost in nanoscale atomistic models. For many new type of materials such as heterogeneous co-planar 2D materials, potentials are not even readily available. Recently, we established the first framework of first-principles multiscale modelling based on machine learning, i.e. machine learning based interatomic potentials (MLIPs), which has been published on Advanced Materials (33, 2102807, 2021). Before this work, our preliminary works for 2D materials has explored promising two-dimensional MoSi2N4 family (Nano Energy, 82, 105716, 2021)with machine learning for photocatalysis properties. In this work, we proposed a robust concept of multiscale modelling of mechanical properties based on MLIPs, that is conveniently and rapidly trainable over short ab-initio datasets. We show that the mechanical and failure responses of complex nanostructures at continuum scale can now be explored with the precision of sophisticated first-principles calculations, with affordable computational cost and without the need for empirical data. Such an approach shows great potential to develop fully automated and coupled platforms to design, optimize, and explore various properties of materials at continuum level, considering atomistic effects and inherent precision of first-principles calculations. To practically illustrate this novel possibility, the mechanical and failure response of graphene/borophene coplanar heterostructures is examined and validated.

At the continuum level for fiber reinforced composites, we developed a double phase fields model for complex failure in fiber reinforced composite (Composite Structures, 193, 115730, 2022). In the model, two different phase fields, namely fiber phase field and matrix phase field, are used for characterizing fiber damage and matrix damage, respectively. The failure mechanisms of fiber damage as well as the other modes in matrix damage are identified through a new strain energy density form that contains four different effective strain variables as well as new effective constitutive tensors. Different damage initiation and evolution criteria can be embedded into the proposed model, as shown in Figure 2, the interlaminar failure can be captured as like the phenomenon during the experiments.